Triangular Numbers
A "Triangular Number" is the sum of all the numbers from 1 to a given number. Such numbers can be represented as dots arranged in the form of an equilateral triangle, in successive lines each having one dot more than the previous.
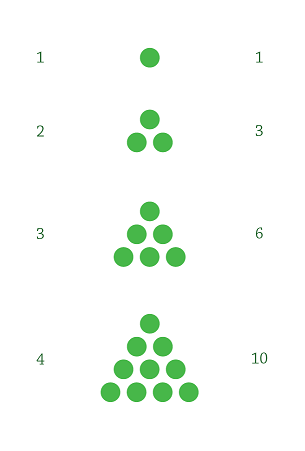
The triangle of 1 is 1, the triangle of 2 is 1 + 2 = 3 (the first literal “Triangular Number”); the triangle of 3 is 1+2+3 = 6, the triangle of 4 is 1 + 2 + 3 + 4 = 10, and so on…
At the base of a triangle of a number appears that number, seen as its “triangular root”. In the representation above, the triangular root is indicated at the left of a triangle, and the triangular number, at its right. So 2 is the triangular root of 3, as 3 is the triangle of 2; 3 is the triangular root of 6, as 6 is the triangle of 3…
This formula can be used to determine a triangular number:
Tn = n (n+1).
2
For example, the triangle of 1 is: 1 (1+1) : 2 = 1 (2) : 2 = 2 : 2 = 1
The triangle of 2 is: 2 (2+1) : 2 = 2 (3) : 2 = 6 : 2 = 3
The triangle of 3 is: 3 (3+1) : 2 = 3 (4) : 2 = 12 : 2 = 6
And so on…
Here is a list of the first few triangular numbers:
1 → 1
2 → 3
3 → 6
4 → 10
5 → 15
6 → 21
7 → 28
8 → 36
9 → 45
10 → 55
11 → 66
12 → 78
13 → 91
14 → 105
15 → 120
16 → 136
17 → 153
18 → 171
19 → 190
20 → 210
